关于粉碎理论的研究成果

粉碎过程从古代人类破碎果壳取栗开始，就在生活和生产中得到了极为广泛的应用。但对粉碎理论的研究进屉却相当缓慢。粉肿皿论研究的内容有被碎物料勒砷过程的机理，粉碎物料需要的功，粉碎产品的粒度分布，以及粉碎过程的速度解析等。

一、粉碎机理

粉碎过程的机理是一个极为复杂的问题。假如一块单独的物料受到突然的打击，通常它将被粉碎而产生较少的大颗粒和很多的小颗粒，同时还有少量中间粒度的颗粒。假如打击的能量增加，大颗粒将具有较小的粒度和较多的数日，而小颗粒的数目将大大增加，但其粒度不变。由此，可以看到小颗粒的粒度与物科的内部结构密切相关，而大颗粒的粒度则与实现的粉碎过程密切相关。

为此海伍德(Hey—wood)在一个小磨机中做研磨煤的一系列实验，其结果如图1—9所示。其中产品颗粒粒度的分布以磨机累积转数的函数表示。原始的粒度分布显示小一个单峰型，它相当于比较粗的颗粒。当粉碎比逐步增加时，这峰型就逐渐减小并且在一特定的粒度产生第二个峰型。这过程一直进行到第一个峰型完全消失时为止。第二个峰型是物料的特征，称为持久峰型，而第一个蜂型称为暂时峰型。

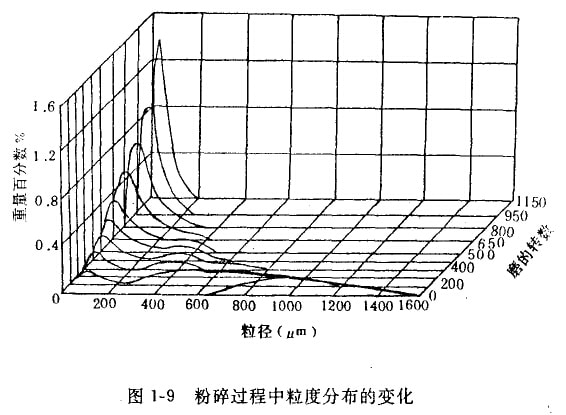
物料粉碎时本身需要的能量与物料内部的结构有关。粉碎过程实际上内两部分组成：首先破开原来存狂的任何小裂缝，其次形成新的表面。有一种物料，如煤具有很多小裂缝并趋向于先沿着这些裂缝破碎，所以大块校小块易于破碎。在破碎一定量细物料时，其表面积的增加远较破碎相物料为甚，因此细磨就需要很大的能量。

从能量的利用观点看，粉碎是一个效率很低的过程，供给粉碎机的能量仅有0.1-2.0％表现在固体表面能的增加上，其余都转变为热能和声能。对要被粉碎物料施加作用力的种类、大小和施加的速率都对粉碎过程的效率有影响。

二、粉碎的功耗学说

确定粉碎过程所需要的能量问题足极其复杂的。因为粉碎的能量消耗与很多因素有关，譬如物料的物理机械性质、所采用的粉碎方法、在粉碎瞬间各物料所处的相互位置、物料的形状和尺寸以及物料的湿度等等。因此，要想用一个完整的严密的数学表达式来解决粉碎过程所需要的能量问题是不可能的。在某些情况下，必须同时广泛地应用实际资料。

关于粉碎需要能量的经典学说有以下三种。

(一)表面积学说

这是雷廷智(Rittinrey)于1867年提出来的，又称雷廷智学说。

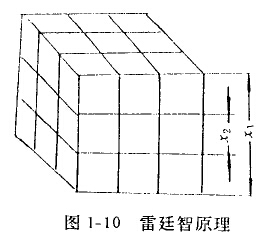
雷廷智原理(图1-10)是以假想的切片进行粉碎的，由此来推导粉碎所需要的能量。

当物料被粉碎后，产生的新的表面积必然比原物料的表面积增多。位于物体表面上的质点与内部的质点不同，由于与它相邻的质点数目不够使它平衡，因而存在着不饱和键能。分裂物体时，必须克服它的内部质点间的内聚力，使内部质点变为表面质点，于是表面上的位能增加，因此粉碎物体要消耗一定做量的能。因而雷廷智认为，外力粉碎物料所作的功，转化为新生表面积上的表面能，故粉碎物料需要的能量与新生表面积成正比。

假设物料的性质是各向均匀的边长为Dcm的立方体(图1-10)。在三个相互垂直的方向上，以间隔d＝D／i的平行平面切立方体，则产生i3个小立方体(d3)，比值i为粉碎比。根据物料备向均匀的假设，则每个单独切片需要相同的能量。

原始表面积为6D2，粉碎后产物的表面积为6i3d2，表面积增加量△S为

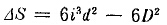
粉碎单位体积物料需要的能量则为

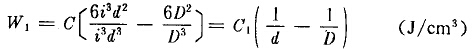
式中C和C?为比例系数。此为雷廷智学说的习惯式。

如果将上式写成

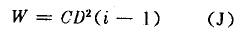
这就清楚地表明，由边长为D的立方体粉碎成边长为d的立方体，所需要的能量随着粉碎比的增加而增加。

在通常情况下，D≥d，即i≥1，则粉碎单位体积物料需要的能量W可写成

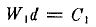
它表明粉碎产品的能量与粉碎产品的粒度成反比。

雷廷智公式仅考虑了破坏分子键的力需要的功。而忽略了产生破坏的弹性变形的功。

由于物料在粉碎前后都是混合粒群，故应用上面公式时应当用它们的平均粒度来计算。选用物料平均粒度的汁算力方法如下。

因为粉碎物料时消耗的能量是物料直径的函数，对于雷廷智学说，此函数的形式为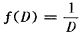。设Dm是粉碎前的物料平均直径。Di是粉碎前物料中个别粒级的直径，Ti是个别粒级的重量百分数。当Dm能够充分地代表物料的粒度时，用它按规定的函数计算得的结果，应当和用个别粒级按同一函数计算的结果的值相等，即

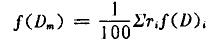
因此对于雷廷智学说中粉碎前物料的平均直径为

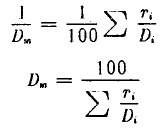
同理可得粉碎后物料的平均直径dm为

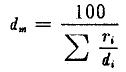
由此可知雷廷智公式中粉碎前后的物料直径都是调和平均径。

(二)体积学说

这是基克(Kiek)于1885年提出来的，又称基克学说。

根据物体受外力引起变形的结果来看，当物体受外力后必然在内部引起应力。随着外力的增加，物体的应力及变形亦随之增大。当应力达到物体的强度限时，则外力稍微增加即使物体破坏。对于脆性物料而言，这种应力与变形的关系，在实际运算时往往取其应力—应变图上曲线所对应的弦来表示。故可认为被秘碎物料受到外力后的变形服从虎克定律。

因此，粉碎边长为D的立方体产生均匀变形时需要的能量为

(三) 裂纹学说

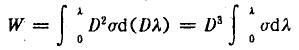
这是邦德于1952午提出来的，又称邦德学说。

表面积学说与体积学说约计算公式，在估算粉碎碎过程需要消耗的能量的值有显著的差别。例如一块要被粉碎的物料，从1000μm粉碎到100μm，再从100μm，粉碎到10μm，然后再从10μm粉碎到1μm。这样接连几次粉碎所需要的能量按(1—29)式计算，后—次都是前一次的10倍，而按(1—32b)式计算前后备次捕要的能量保持不变，后者是与实验扣矛盾的。因此，邦德提出了所谓第三学说。邦德认为，粉碎物料时，外力作用的功首先是使物体发生变形，当局部变形超过临界点时即生成裂纹，裂纹形成之后，储在物体内的形变能陵裂纹扩展并生成断面。输入功的一部分转化为新生表面的表面能，其余部分转变成热损失。因此，粉碎物料需要的能量，应当考虑变形能和表面能两项。对于第一次破碎需要的能量，根据基克学说与D³成正比。接着再进一步粉碎，根据雷廷智学说与D³成正比。因此，粉碎所消耗的总能量一定在D³与D²之间，邦德随意地取为。因此粉碎单位体积物料消耗的能量与欲碎物料的粒度关系为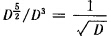。所以把单位体积物料出粒度D粉碎到d需要的总能量为

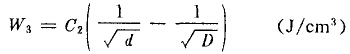
上述的三个学说，各看到粉碎过程的一个方面。基克学说注意的是受力发生的变形，邦德学说注意的是裂纹的形成和发展，雷廷智学说则注意的是粉碎后新生成的表面积。因此，它们都有片面性，但互不矛盾，却互相补充，每一个学说只能在一定的粉醉范田拉为适用。物科在破砰时的破碎比不大，新生表面积不多，形变能占主要部分，故基克学说铰为适用。粉磨时粉好比很大，新生表面积多，表面能是主要的，因而雷廷智学说较为适用。在破碎和粉磨之间，在中等粉碎比的情况下，邦德学说较为适用。这个论断已为胡基(HuKKi)的试验所证实。在上述中间范围内邦德学说较为接近。

粉碎过程是很复杂的，这些学说对许多影响因素未作考虑。例如物料的结晶缺陷、裂缝和节理、湿度、粘度、不均匀性，以及物料间的相互摩擦和挤压等，都会影响到物料的强度，从而也就会影响粉碎时消耗的能量。因此，即使各学说在适用的范围内，也只能得到近似的结果，还须用实际资料来校正。故而各种类型的破碎粉磨机械都有各自的功耗公式。