粉碎过程速度解析概述

粉碎过程耗能很多，所以过去对粉碎过程的研究主要是研究功耗问题。现在这方面的研究已取得较多进展。然而，单纯功耗理论不是全部粉碎理论，功耗—粒反函数亦不适于描述整个粉砰过程。因而有必要研究粉碎设备的给料和排料之间的关系。

由图1-9可知，粒度分布的变化是不连续的，而是具有若干峰形曲线的多组成分布。要研究第1组成的粒子是如何进入第2、第3或第n组成的，即要确定各组成间的移动速度，也就是用解析的方法确定速度常数。这是模似化学反应的考虑方法。

胡基、谢得拉切克和巴斯提出了下列联立方程式

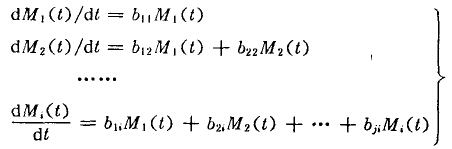
式中M(t)为粉磨t时间后粒度x的筛下量，b(i≠j)表示第j组成的粒子粉碎后进入第i组成移动的质量比例人表示第i组成的粒子粉碎后原粒子的残留比例；b表示第i组成粒子粉碎成比第i组成小的粒子的移动比例。

方程织(1—43)的解如用行列式表示时，则粒应分布等可用矢量表示，而颗粒各粒度组成间的移动速度可用矩阵表示。

这是将粉碎速度论和粉碎产物粒度分布联系起来的有效方法。布劳得本特和卡尔考特于1956年提出了如下的粉碎过程的矩阵表示法。

卡尔考持以任意几何间隔单位。(如筛比)来划分粒度组成，并把1-a。a-a²，a²-a³，…各间隔的频率看作列矢量，给料粒度的分布式定义为

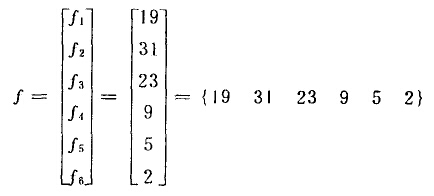
为了研究方便，利用上述表示方法，设粒度分布矢量f＝｛30  20  10｝，并设实际粉碎中正好有一半粒子受到粉碎，即｛15  10  5｝受到了粉碎作用。由表1—9可知，该表最下面总计栏内为粉碎前的粒度分布矢量。经过粉碎后，各粒级的颗粒向更小的粒级变移，其变移的比例(百分数)表示在纵列栏内。例如在开始时处于1-a之间的颗粒，经粉碎后在1-a间隔内残留6，转移到a-a²间隔的为3，a²-a³间隔的为3，而其余的(3)则转入比a³更小的间隔。其次，原来处于a²-a³间隔的颗粒经粉碎后在a-a²间隔残留4，转移到a²-a³间隔的为2，转移到比a³更小间隙的为(4)。各粒度相互之间的变化对最初的｛15  10  5｝的比例可表示如下

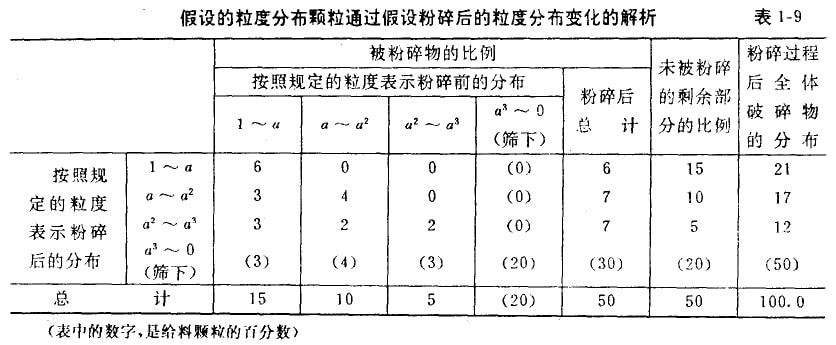
此矩阵表示了粉碎前后各组成粒子的移动状态，即表示了粉碎特性，故将其定义为碎裂矩阵B，或称碎裂函数。卡尔考特假定B为如下阶梯矩阵

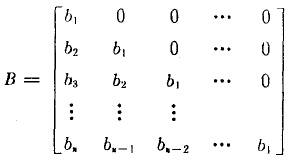
由表1—9可见，粉碎后总计栏表示受粉碎作用的粒子粉碎后的分布。如加上未受粉碎作用的部分，则可得最后一列所示的粉碎后全部粒子的分布，即粉碎作用产生了｛30  20  10｝—｛21  17  12｝粒度分布的变化。

如将这一过程用矩阵表示则可写成下式

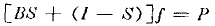
式中P为初碎产物的粒度分布列矩阵，I为单位矩阵，S为选择函数。

进入粉碎过程的各个粒级受到的碎裂见有随机性质，即有的颗粒受破裂多些，有的少些，有的则直接进入产品而不受破裂，这就是所谓选择性或称概率性。用S表示受到粉碎作用颗粒的比例，即粉碎概率，称为选择函数，并假定为对角阵

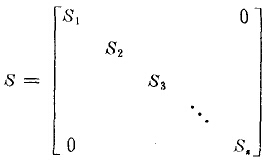
在本例中S=0.5。

本例P的计算如下

上述是一次粉碎的情况。矩阵模型是把粉碎过程看作一系列川继发生的粉碎事件，后一次的给料是前一次的产品，对于二次反复粉碎则为

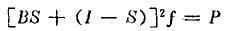
因而在进行n此反复粉碎后，则成为

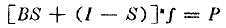
由于缺少提供关于物料固有碎裂特性的非破坏性试验方法，所以碎裂函数B是一个很难用实验方法确定的两数。但是，在给定设备中粉碎特定物料时，存在一种持有的产品粒度分布形式，它和被碎料的性质和对其施加作用力的条件有关。布劳得本持和卡尔考特于1956年建议采用罗辛—拉姆勒方程的修正式表示，即

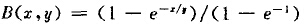
式中B(x，y)，表示原来粒度为y经粉碎后小于x粒径的质量分数。因而有的学者把破裂函数B又称为分布函数。

对于选择函数S来说，与粉碎机械的粉碎机理、碎料的性质和粒径等有关。但是至今还没有理论解，只是用实验的方法在特定粒度范围内有如下的关系

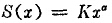
式中x为粒径，K和α为常数。