岩矿破碎的强度理论

岩矿破碎的强度理论 目录导航：剪切破坏强度理论   脆断破坏的强度理论   裂纹扩展理论

岩矿是一种多元力学结构的复杂体系，要从理论上弄清它的破坏原因是十分困难的。现代固体力学也无法指导岩矿的实际破碎工程计算。因此，岩矿的破碎只有采用力学强度理论来解决实际问题。这就是说，既然力学在理论上说不清岩矿为什么会破坏， 就干脆避开岩矿为什么会破坏的问题，而以某种力的状态作为破碎的终极原因，釆用直接测量的办法，测量岩矿断裂的条件。但是，实际的测量也总是有限的，在最简单的情况下是采用单位断裂面积上受力的极限——极限强度来表示断裂条件。岩矿的极限强度是通过实际测量的途择得到的。然而，岩矿的应力形式又不是单一的，有时是多种形式的应力同时存在，而且每种应力下岩矿破坏的极限强度是不相同的。那么，在多种应力或组合中，究竟是哪一种应力、应变的极限状态或其组合导致破碎的发生？不同的研究者认识不同，观察研究的角度不同，因而就有不同的结论，于是，出现了不同的岩矿破碎的强度理论。下面介绍几种常见的岩矿破碎的强度理论。

(1)剪切破坏强度理论

剪切破坏强度理论认为，物体中只要剪应力增长到某个极限，物体就要产生大的塑性变形而屈服、滑 移或破坏。这种理论甚至认为，一切破坏都是由剪切造成的。属 于这一理论的有最大剪应力理论、内摩擦理论、八面体剪应力理 论等。按最大剪应力理论，当存在三个主应力且σ₁＞＞σ₂＞σ₃，并以压应力为正，由力学分析知道其最大剪应力τ_m为：

式中σ₁及σ₂分别为最大和最小主应力。当

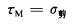
时，物体也就发生破坏。

固体的破坏理论中，剪切破坏强度理论是研究得比较多的，但此类破坏适用于金属等塑性材料的破坏，而不适于岩矿材料的破坏。岩矿材料一般硬而脆，几乎没有塑性。大多数岩矿也是不可 压缩的，其体积压缩率的数量级约为10^-6或10^-7,即增加 101. 325kPa时岩矿的体积比较其原始体积减小百万分之几或千万分之几。对岩矿来说，往往屈服也就破碎了。而且，按最大剪应力理论推论，材料的单向抗拉强度和抗压强度相等，这个结论对于岩矿是差得太远了，岩矿的抗拉强度小于抗压强度的十分之一左右。因此，剪切破坏强度理论对于岩矿材料的破坏是不合适的。

(2)脆断破坏的强度理论

此理论认为，在三个主应力全是拉伸的情况下，以其中最大拉应力（σ₃）是否达到某一临界值来作为判断物体破坏的依据，而对其余两个拉应力则不考虑；在拉应 力和压应力共同作用的情况下，则以最大拉伸应变达到某个限度 作为物体是否发生断裂的依据，而这个限度可以通过试验确定。最大拉伸应变ε₃为:

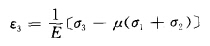
式中           E——弹性模量；

      μ——泊桑比；

σ₁、σ₂、σ₃——三个主应力。

对脆性大的矿物而言，ε₃值不大，韧性大的矿物ε₃较大，即脆性矿物比韧性矿物易破碎。

按照此最大拉伸变形理论必然推得关系：

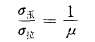
此式中的泊桑比μ值平常在0.2~0.5范围，故脆断的抗压强度是 抗拉强度的2~5倍。但对岩矿来说，此数值显著小于实际数值, 这也许是由于实际岩矿材料中隐藏着裂隙或脆弱面的缘故。与前面的剪切破坏强度理论相比，脆断破坏强度理论对岩矿材料要更适合一些。

(3)裂纹扩展理论

裂纹扩展理论是由A.格里菲斯于1921年提出来的。他提出这一理论是基于破碎玻璃实际耗费的能量只有理论数值的三万分之一这样一个事实。他做的实验证明，脆性材料中由于内部存在细微的裂纹缺陷，抗拉强度将大幅度地降低。他提出的假说认为，试件内存在微裂缝，而裂缝尖端有高度的应力集中，以致使裂缝扩展并造成破坏。格里菲斯提出计算临界载荷的公式为：

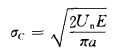
式中         Un——表面能；

            E——弹性模量；

            α——裂缝之半的宽度。

裂缝扩展理论比较适合岩矿材料的破坏，因为岩矿材料既隐藏有缺陷，又具有脆断的待性，破坏过程有裂缝产生和扩展。

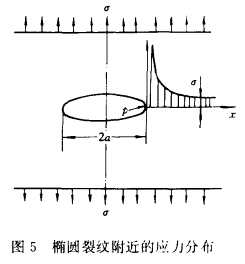
图5表示一个椭圆裂纹附近的应力分布情况。从图可见，在离孔远处，应力分布受孔的干扰很小，基本上是均匀分布的。在长轴的两端点上，有高度应力集中，而在短轴两侧，应力被卸除，形成低压区。当椭圆的短轴长度衰减至零时，便是一条长度为2α√σπ的裂纹。当ρ≤α时，最大应力为：

形成低压区。当椭圆的短轴长度衰减至零时，便是一条长度为2α的裂纹。当ρ≤α时，最大应力为：

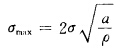
而裂纹附近的各种应力及位移都和Yσ√πα有关，Y是和裂纹方向、型式、尺寸、位置有关的一个系数。用符号K来表示Yσ√πα称为应力强度因子。Y值可由专门的分析得到，在手册中可以查到。

当载荷σ或裂纹长度α达到某一临界数值，正好足以使裂纹 发生扩展，在这种临界状态下的应力场强度因子就称为断裂韧性 Kc,它是有裂纹材料断裂难易的一个判据。裂纹尖端附近的应力 场强度因子Kc达到什么程度时裂纹才会扩展？单凭力学是冋答不了这个问题的，和前面的力学强度理论一样，必须通过实际测定才能给出断裂韧性的数值来。

这里必须强调指出，岩矿材料由于自身力学性质的特殊性，它的破坏与材料力学中的梁、轴、柱等的破坏有着本质的区别，故用材料力学中拉、压、剪应力极限作破碎判据就显得不完善。材料力学中研究的各种材料，其抗压、抗拉、抗剪和抗弯的极限强 度对某种材料而言几乎是个常量，即每种材料均有自己的材料常 量。但岩矿则不同，不同矿体中产出的同种矿石，或同一矿体中 不同部位产出的矿石，其力学强度均不相同，很难确定岩矿的力 学性质常量，即使同种矿石的某种极限强度测定量值波动范围也 很大。这就使岩矿的破碎判据很难确定，即使是前述的三个强度理论，仍然不成熟和不完善，只有借助于试验测量来确定岩矿的 极限强度。尽管如此，三个破坏的强度理论均明确指出，岩矿的破坏是由于矿块某种应力超过极限强度所引起的，而且，三个理论也为深入研究岩矿的破碎问题提供了有价值意见。

上述的研究现状表明，当要对岩矿的破碎作精确的工程计算时，如要计算球磨机中不同矿块破碎所需的精确破晬力时，靠力学计算是无法解决问题的，也无可靠的岩矿力学常量可供使用，最科学的办法是按破碎工程的需要进行实际测量。由于各选厂处理的矿石力学性质不一样，若要计算所需的精确破碎力，只有对该厂矿石进行实际测量。只有这样才能精确选择钢球尺寸。