矿物的机械强度对磨碎的影响

研究矿物在磨碎过程中的磨碎行为，首先应该研究矿物破碎过程发生的判据，进而才能说明矿物的破碎及影响矿物磨碎的因素。

一、矿物的机械强度对磨碎的影响——岩矿破碎的判据

对于固体物料的破碎，至今仍无完善的理论解释。虽然晶体破碎理论能比较深入地说明品体受力后的变形及破坏原因，且能定量地进行计算，但自然界实际矿物晶体由于存在各种宏观或微观缺陷，以及成矿地质作用的千差万别，常导致理论计算与实际所需破碎力之间存在很大的出入。因此，在研究岩矿破碎问题时，虽然可以运用力学来分析受力状况，但是需要多大的力或多大的力的组合才能导致破碎仍然是个不确定的问题。所以单靠分析力的状况并不解决问题，还必须借助实际的测量。这就是说固体理论还难以用于具体的工程计算，在工程技术上普遍采用的则是力学强度理论，所采用的办法是直接测量，以便避开固体破坏，而以某种力的状况作为破碎的终极原因。实际测量在最简单情况下常用单位断裂面上受力的极限一一极限强度来表示断裂的条件。由于岩矿的极限强度是通过实际测设得到的，所以可以用来检验理论是否正确，如果理论正确，就可用来回答各种情况下 岩矿的破碎能否发生。

过去一般是将材料力学中的强度极限作为岩矿的破碎判据，但岩石是由不同坚固程度的矿物组成，并且常常有许多脆弱面， 破碎载荷又常是动态的集中力，并且，在岩石破碎中还要研究破碎程度和范围，由于岩矿的破碎过程和材料力学中梁、轴、柱的破坏有着本质的区别。因此，只用拉、压、剪应力极限作判据就显得很不充分。近年来在岩矿破坏判据研究方面已出现了若干种破坏的强度理论，例如有剪切破坏强度理论，脆断破坏强度理论及格里菲斯的裂缝扩展理论等等，但仍不成熟不完善，即是说， 岩矿破碎的判据目前尚不完善，更谈不上具体数值的大小。为了实际应用，现实可行的解决办法仍是在规定条件下实际测量岩矿的坚固性指标。

尽管岩矿破坏的判据不甚清楚，但知道矿物的破坏是由矿块内的某种应力超过极限强度所引起的，所以下面就几种常见的破坏强度理论进行一些分析讨论。剪切破坏理论对粗性材料比较合适，按照剪切破坏理论并可以推论出单向抗拉强度等于单向抗压强度的结论。但这对岩石的彼坏就相差太远了，因为岩石的抗拉強度约只有抗压强度的十分之一。脆断破坏理论是在三个主应力拉伸的情况下，看最大拉应力是否达到某一临界值作为判断物体破坏的侬据，而对其他两个拉应力则不考虑；在拉应力和压应力共同作用的佶况下，则以最大拉伸应变达到某个限度作为物体是否发生断裂的依据，且这个限度可通过试验确定。最大拉伸应变ε3：

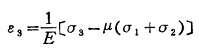
式中 E——弹性模量；

μ——泊桑比；

σ₁、σ₂、σ₃——三个主应力。

对于脆性大的矿物而言，ε₃值不大，而对韧性大的矿物ε3值亦较大，即脆性矿物比韧性矿物容易破碎。按最大拉伸理论可以推得脆断的抗压强度是抗拉强度的2～5倍，对岩石来说此数值还小于实际数值，这也许是实际矿石中隐藏着裂隙或脆弱面的缘故。

裂纹扩展理论对岩石比较适合，岩石既有缺陷，又属脆断，破坏过程有裂纹产生及扩展。格里菲斯提出计算临界载荷值的公式为

式为

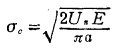
式中Un—表面能；

E——弹性模量；

a——裂隙之半的宽度。

从上述分析可以看出，不论哪种破坏强度理论，岩矿的破坏均与自身的机械强度有关，均要使某种应力达到某一个极限时岩石才会发生破坏，所以，研究岩矿破碎问题时不能离开岩矿的机械强度。

二、矿物的机械强度对磨碎的影响——选择性磨碎的判据

前面对岩矿破碎判据的分析说明，玻碎过程的发生是由于岩矿内某种应力已达到了相应的极限强度，而岩矿自身的应力极限强度又是由自身的力学性质所决定。前已述及，岩矿的硬度、韧性、解理及结构缺陷等共同决定着它的力学性质，通常并以机械强度这一综合指标表征岩矿的坚固性。机械强度大时因承受压力的极限强度亦大，破碎时就较困难；反之，机械强度小者，破碎就容易。

破碎行为的发生不仅与岩矿的机械强度有关，而且与破碎过程的其他条件有关。由子破碎行为的发生带有随机的性质，因略宜用统计的办法研究破碎行为。现用破碎概率Wp来表征破碎行为出现的概率，V．V．卡码金提出，破碎的概率Wp与岩矿的机械强度σ有如下关系

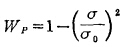
式中σ₀——应力圆半径。

如果有A、B两种矿物，它们的机械强度σ_A及σ_B不同，设σ_A比σ_B大，这两种矿物遭受相同的破碎作用时则破碎的概率为:

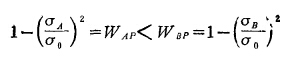
即是说，机械强度大的矿物破碎概率小于机械强度小的矿物。由于机械强度的差异导致了矿物破碎概率的差异，也就导致了矿物磨碎行为的差异。

V．V．卡玛金还提出了磨矿时矿物的选挥性破碎的判据K为：

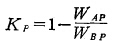
由上式可见，如果两种矿物的机械强度σ_A及σ_B相同，它们的破碎概率W_AP及W_BP也相同，这时K_P=0，即A、B两种矿物混合磨碎时无选择性可言。当两种矿物的机械强度σ_A及σ_B不等时，W_AP和W_BP亦不等，这时K有一确定值，表示存在破碎的选择性。显然，K值愈大，破碎的选择性愈大，K值愈小破碎的选择性也愈小。但是，直接以K值大小来判断选择性破碎的程度在实际破碎工程应用上目前还比较困难。由于发生选择性破碎时 会使两种矿物粒子存在粒度差，所以直接以粒度差的大小来判断选择性破碎程度大小可能更便于实际工程上的应用。如果以δ_c表示相对粒度差，则由两种矿物粒子的加权算术平均直径d_A及d_B就可算出δ_c：

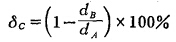
从实际资料中可以认为：

δ_c=5~10%选择性磨碎现象较为显著；

δ_c=10~30%选择性磨碎现象显著；

δ_c＞30%选择性磨碎现象很显著。

当然，也可以考虑以某一指定粒级（如一200目）含量的差值来判别选择性磨碎现象是否显著，若差值显著地超出粒度測定误差波动值就应该认为较显著地存在者选择性磨碎现象。